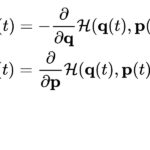Articolo di Massimo Scalia (CIRPS) e Carlo Cattani (Engineering School, DEIM, University “La Tuscia)
Abstract
Uno dei modelli matematici più semplici per la crescita di una popolazione è la funzione logistica di Verhulst, che in questo lavoro viene applicata alla previsione della crescita dei contagiati da Covid-19 nelle aree italiane più colpite: la Lombardia e le città di Bergamo, Brescia e Milano. A causa di una sua certa “rigidità” la curva logistica fornisce una previsione precisa solo quando la velocità di crescita dei contagi esibisce un picco molto marcato, come ad es. per lo Hubei e la Cina o come ci si può attendere nelle influenze stagionali. Inoltre, per tener conto dell’alone di indeterminatezza dei dati giornalieri è opportuno considerarli come i valori di un moto browniano, sostituendo al comportamento logistico una serie teorica di dati che approssimi bene quella reale. Il giorno in cui la serie teorica si sovrappone a quella dei dati reali è il giorno a partire dal quale si ha una stima attendibile sull’evoluzione del fenomeno. I calcoli per la serie teorica richiedono un programma numerico, allora, per maggior applicabilità, viene fornita per la determinazione del giorno “cruciale” un’approssimazione lineare, una sorta di tangente alla curva dei dati, in grado di dominare la successiva evoluzione dell’infezione.
One of the simplest mathematical models for population growth, the Verhulst logistic curve, is provided to make some prediction on the curve growth of Covid-19 pandemic spread. However, due to the “rigidity” of the logistic curve, a precise forecast can be done only under some very special and well-determined conditions, such as in the case of the time evolution of the infection in China, or, maybe, for seasonal flues. In general, taking into account the halo of randomness associated to each reported daily data and treating the latter as a value of the Brownian motion, we can replace the logistic behavior with a theoretical time series, fairly approximating the real data series. The day of the overlapping between theoretical and real series is what we were looking for, as we show applying this method to Lombardy and its more affected cities: Bergamo, Brescia and Milan. To shorten the calculations to obtain the theoretical values, a linear approximation is provided, a sort of geometric tangent to the data curve in the crucial day, able to dominate the data of the successive evolution of the infection.