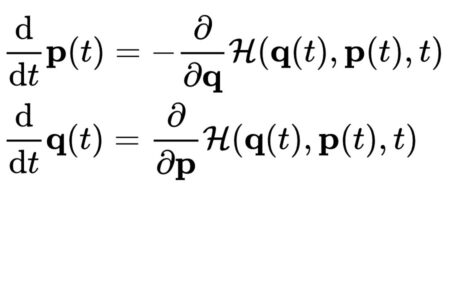Articolo di M. Scalia, A. Angelini, F. Farioli, GF. Mattioli, O. Ragnisco, M. Saviano
Abstract
The severity of the two deeply correlated crises, the environmental and the economic ones, needs to be faced also in theoretical terms; thus, the authors propose a model yielding a global “stationary state”, following the idea of a “steady-state economics” by Georgescu-Rogen and Herman Daly, by constructing only one dynamical system of ecological and economic coupled variables. This is possible resorting to the generalized Volterra model, that, translated in the Hamiltonian formalism and its Hamilton equations, makes possible to “conjugate” every pair of variables, one economic, the other one ecological, in describing the behavior in time of a unique dynamical system.
Applying the model to two of the most relevant ecological-economic pairs of variables leads to a suggestive geometry in the “phase space” of the model: the trajectories are curves wrapping a “donut”, their set is the “stationary state” we were looking for. Those trajectories are “quasi-periodic motions”, characterized by two frequencies, for whose values a good estimate is provided in the “small oscillations” approximation. A more general, but more abstract, “stationary state” is defined by virtue of the stability of the solutions of the Hamilton equations, just in this article recognized.
The global character of the model is assured when world data of variables are used. A very interesting feature of the model is that the path to a scenario of sustainability is given in terms analogous to the Newtonian Dynamics.
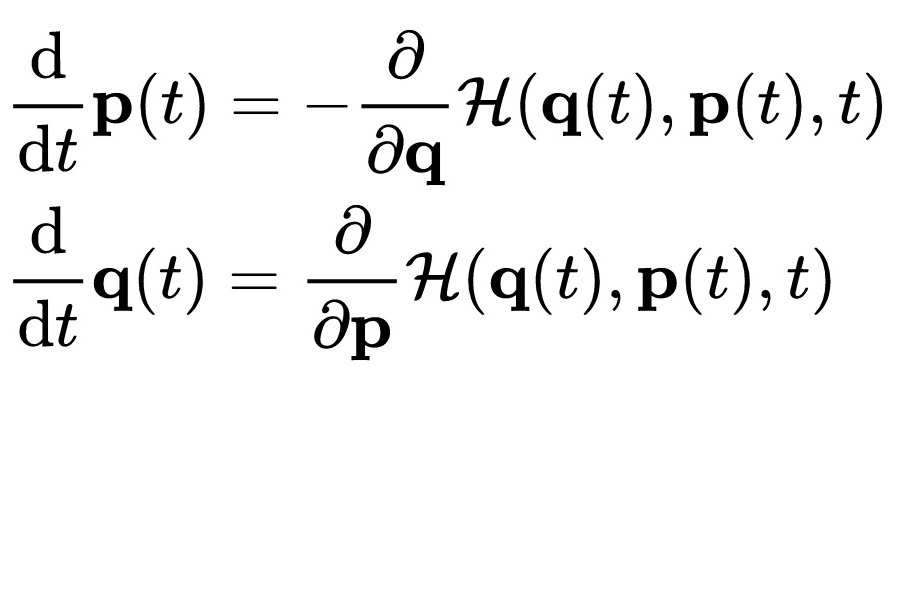
La severità delle due crisi globali fortemente intrecciate, quella ambientale e quella economica, va affrontata anche in termini teorici; per questo gli autori propongono un modello di “stato stazionario” globale e, seguendo l’analoga idea di Georgescu-Rögen e Herman Daly, costruiscono un unico sistema dinamico di variabili ecologico-economiche accoppiate a due a due. Ciò è possibile se si ricorre al modello generalizzato di Volterra che, trascritto nel formalismo hamiltoniano e nelle equazioni di Hamilton, consente di “coniugare” ogni coppia di variabili, una ecologica e l’altra economica, nel rappresentare l’evoluzione nel tempo di un unico sistema dinamico.
L’applicazione del modello a due delle più rilevanti coppie ecologico-economiche porta a una suggestiva rappresentazione geometrica nello “spazio delle fasi” del sistema: le traiettorie dell’evoluzione sono curve che si avvolgono attorno a una “ciambella”, il loro insieme è lo “stato stazionario” che stavamo cercando. Queste traiettorie sono moti “quasi-periodici”, caratterizzati da due frequenze per le quali possono esser fornite delle buone stime nell’approssimazione delle “piccole oscillazioni”.
Anche quando le coppie di variabili sono più di due e viene meno la rappresentazione della “ciambella”, si può definire, più in astratto, uno “stato stazionario” in virtù della stabilità delle equazioni di Hamilton del modello, proprietà che viene dimostrata proprio in questo articolo.
Il carattere globale è assicurato quando si fa ricorso ai dati mondiali delle variabili usate. Una caratteristica molto interessante del modello è che l’evoluzione nel tempo verso uno scenario di sostenibilità è data in termini analoghi alla dinamica newtoniana.